|
|
|
Guionnet Awarded 2009 Loève Prize
The Itô prize has been created in 2003 by an initiative of Philip Protter on
the occasion of Professor Kiyosi Itô’s 88th birthday, a special date
in the Japanese tradition. It celebrates the fundamental contributions of
Professor Itô to probability. This is the first edition following the sad event
of his passing away, and we wish to honor his memory.
Every two years, the editorial board of the journal Stochastic Processes and
Their Applications (SPA) selects one article published in SPA during the last
two years, which the board considers to bring a substantial contribution to the
subject. By the way, I take this opportunity to mention that Sylvie Roelly, our
chair today, received the Third Itô prize, in 2007 (jointly with Michele
Thieullen).
I am here today because this prize was decided by the past editorial board of
SPA, whose term ended a few months ago. On behalf of the journal Stochastic
Processes and their Applications, it is my big pleasure to award the fourth Itô
prize to Marc Wouts, from the University of Paris 13, for the paper “A coarse
graining for the Fortuin-Kasteleyn measure in random media”.
Let me add a few words on this decision:
Renormalization procedures play a fundamental role in the description of the
equilibrium phase coexistence in statistical mechanics models. In the classical
case, remarkable progress has been achieved in the 90s, following the
development of an efficient coarse graining description by Agoston Pisztora. The
extension to random environments is difficult, and requires truly new insights.
The results and tools developed in the article show a wide range of potential
applications.

Finally, I would like to transmit to the recipient the kind regards of Professor Itô’s family, and before passing on to Thomas Mikosch, the journal editor, it is my great pleasure to call Marc Wouts to receive a certificate of our recognition for his work.
Maria Eulalia Vares, Rio de Janeiro

Marc Wouts entered École Normale Supérieure as a student in 2000 and
graduated then at University Pierre et Marie Curie. He obtained his Masters from
the University Paris Sud and then started a Ph.D. thesis at the University Paris
Diderot under the direction of Thierry Bodineau. His research was concerned with
the effects of dilution in the Ising model on the phenomenon of phase
During that time, he was solicited for teaching duties at University of
Barcelona, ENSAE Paris, University Paris Ouest. Last year he obtained a teaching
and research position (maître de conférences) at University Paris Nord.
The award winning paper "A coarse graining for the Fortuin-Kasteleyn measure in random media" addresses the issue of establishing a renormalization scheme for the dilute Ising model in the regime of phase transition. The Fortuin-Kasteleyn representation of the Ising model is an adequate framework for answering such a question as it provides a joint distribution on spins and edges variables, in which the geometry of clusters govern the structure of spins. An effective description of the geometry of those clusters for the non-dilute case was given by Pisztora [PTRF 1996] and permitted a rigorous description of complex phenomena like phase coexistence in three dimensions for the Ising model. The above paper is a generalization of the work of Pisztora for a dilute model. An additional layer of randomness is introduced: the interaction strength between neighbour spins are i.i.d. positive and bounded random variables. Although being a generalization of the uniform model, this random media version lacks an essential property of the former: the DLR equation. This makes Pisztora's scheme of proof ineffective and the author has to resort to advanced probabilistic and geometrical constructions to bypass this difficulty. The same controls as for the uniform case are established. It is proven that blocks are
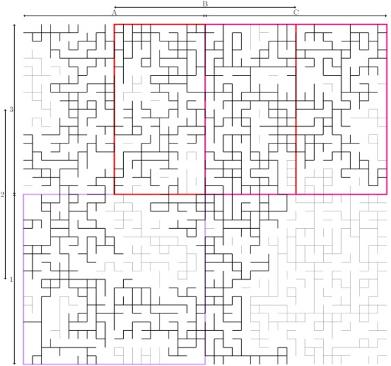
good (see Figure 1) with probability close to one when the block size is
large, under an assumption of slab percolation under the averaged measure.
Controls on the density of the cluster are inferred as well. This
renormalization framework was latter applied [CMP 2009] to the study of phase
coexistence in the dilute Ising model.
Figure 1: An insight at renormalization. The figure presents a
realization of independent percolation of parameter p=0.52 on a 40x40 square
lattice. A block is good when it contains a cluster that connects every edge of
the block, and when this cluster is the only one that has a diameter larger than
half the size of the box. The block A1 is not good because it contains two
clusters of diameter greater than 10. Blocks B3 and C3 are good. Notice that
overlapping good blocks share the same main cluster. In the paper is it shown,
under the slab percolation assumption, that most blocks are good when their size
is large enough. This provides an effective control of the geometry of the main
cluster.
Marc Wouts, Paris
The 2009 Line and Michel Loève International Prize in Probability is awarded
to Alice Guionnet of the École Normale Supérieure de Lyon. The prize, which
carries a monetary award of $30,000, will be presented at a ceremony in Berkeley
in October 2009.
She received her Ph.D. in 1995, advised by Gerard Ben Arous. Her thesis dealt
with Langevin dynamics in the Sherrington-Kirkpatrick model of spin glasses, via
a large deviations approach. The study of dynamics for complex systems (spin
systems, particle approximations to the nonlinear filtering equations and spin
glasses, where logarithmic Sobolev inequalities in particular and concentration
of measure methods in general are very relevant), and more specifically the
study of aging phenomena, continue to be a component of her research to this
day, with important collaborations with Zegarlinsky, Ben Arous, Dembo and Mazza.
Maybe more important, it also naturally lead her to what would become her main
area of research and best known work, namely the study of large random matrices.
Starting with a proof of the large deviations principle for the spectral measure
of Wigner matrices (with Ben Arous), which helped to bring to the attention of
probabilists the concept of non-commutative entropy coined by Voiculescu, she
quickly realized that dynamics and concentration techniques can be adapted to
this context and yield a systematic approach to many open questions. Results
include the full large deviation principle for the spectral measure of
generalized Gaussian matrices and concentration of the
spectral measure in more general models (with Zeitouni), and later applications
to the study of random matrix models, which had long been studied non-rigorously
in mathematical physics. She has found rigorous arguments and elucidated
connections with other mathematical fields, in topics such as first and second
order expansions of the free energy and the connection with maps enumeration;
stochastic analysis for random matrices and Dyson's Brownian motion; connections
with ”free probability”; and most recently, the study of planar algebras. A
partial list of collaborators here includes B. Collins, V. Jones, D.
Shlyakhtenko, and her students M. Maida and E. Maurel-Segala. This has been an
extremely active field over the last years, with many workers pursuing many
partly overlapping techniques and problem domains, and her lecture notes from
courses in 2003 and 2006, together with a forthcoming monograph (with Anderson
and Zeitouni), have helped to bring welcome clarity to the field.
About the Prize: The Prize commemorates Michel Loève, Professor at the
University of California, Berkeley, from 1948 until his untimely death in 1979.
The Prize was established by his widow, Line, shortly before her death in 1992.
Awarded every two years, it is intended to recognize outstanding contributions
by researchers in probability that are under 45 years old.
David Aldous, Berkeley