|
|
|
On the Life and Mathematics of K. Itô and W. Döblin
Kiyosi Itô was born on September 7, 1915, in Mie prefecture, Japan. His father was a high school teacher on Japanese and Chinese literature. Kiyosi Itô passed away on November 10, 2008, at the age of 93. He entered Tokyo University, Department of Mathematics, in 1935 and graduated from it in 1938. After graduation, he worked in the Statistical Bureau of the Government in Tokyo until he became an Associate Professor at Nagoya University in 1943. During this period, he was also awarded a research grant of the government, and thanks to the kindness of the head of the Bureau, he was able to spend enough time on his research in the Department of Mathematics at Tokyo University.
In 1942, Itô published his first two papers [I1, I2]. The first one [I1]
presented what is nowadays called the Lévy-Itô decomposition of a Lévy process.
The second one [I2] was in a mimeographed handwritten Japanese journal issued
from Osaka University and contained already the stochastic integral, stochastic
differential equations with Lipschitz coefficients and Itô's formula. It is
still hard for me to imagine how such big results could be attained in such a
short period of time starting from almost nothing.
In a film, K. Itô explains how he started to work in probability theory: “In
1935 I visited with my classmates Kodaira and Kawata a bookstore, a foreign book
dealer in Tokyo, and encountered Kolmogorov’s book [K1]. Kodaira told me that
this is said to be Probability Theory. Of course, I knew what the word
“Wahrscheinlichkeitsrechnung” meant. But I did not take it seriously at that
time. After 1937, I got gradually interested in Probability Theory and realized
that this book by Kolmogorov is what I had been truly looking for. Since then, I
have kept it as the firm cornerstone in my mathematical thinking while advancing
ahead. From my high school days, I was very fond of mathematical descriptions in
mechanics. I preferred Mathematics to Physics as it is more rigorous, but I was
also concerned with the practical use of mathematics.
In the mathematical community of Japan, Probability Theory was not recognized as
an independent branch of mathematics. I strongly felt that Probability Theory
should be of its own interest and of its own significance as a new field in
science, not just something subordinate to other branches of mathematics like
Fourier Analysis, Differential Equations, etc.
When I came across the book of P. Lévy [L] where the processes of independent
increments were studied on the sample path level and the Lévy-Khintchine formula
was then derived by taking an
expectation, I was extremely impressed. I keenly realized that Probability
Theory must be developed in this way. But, for P. Lévy, compound Poisson
processes were well-known objects that had arisen in practical problems of
insurance and he might have reached a general Lévy process quite constructively
as their possible limit without big surprise. I then made the presentation in
[L] more rigorous with a help of the idea in [D] on the concept of the regular
(càdlàg) version of the sample path.
With this experience, I turned to a construction of a Markov process
interpreting Kolmogorov's analytic approach in [K2] in the following way: the
sample path 
of a
Markov process (in the diffusion case) is a continuous curve possessing as its
tangent at each time instant t the infinitesimal Gaussian process
I spent almost one year by repeatedly drawing pictures of such curves before
arriving at a right formulation of stochastic differential equations.
My first daughter was 2 years old, and I remember that she said “Daddy is always
drawing pictures of kites!” However, such a drawing convinced myself that a
general coefficient of the equation ought to be a functional of the whole past
of events
, a process
adapted to a filtration
in the modern term,
and that it is really an infinite dimensional and non-linear object.”
A few years after the end of the Second World War, Itô sent J.L. Doob a
manuscript of an extended English version of his 1942 Japanese paper asking for
a possible publication in the USA. No Japanese journal at that time allowed such
a long paper due to the shortage of paper. Doob immediately appreciated its
significance and kindly arranged its publication in [I3].
Itô became a Professor of Kyoto University in 1952. He was also a Professor of
Stanford University (1961-1964), Aarhus University (1966-1969) and Cornell
University (1969-1975), respectively. During these periods of being abroad, Itô
occasionally came back to Kyoto and gave very influential lectures on branching
processes, point processes of excursions and so on. He retired from Kyoto
University in 1979. He was then a Professor of Gakushuin University, Tokyo,
until 1985.
From 1954 to 1956, Itô was a Fellow of the Institute for Advanced Study at
Princeton University, where W. Feller had started his investigation of the one
dimensional diffusion processes.
He tells the following about this period: “When I was in Princeton, Feller
calculated repeatedly for a one dimensional diffusion with a simple generator
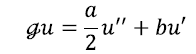
the quantities like
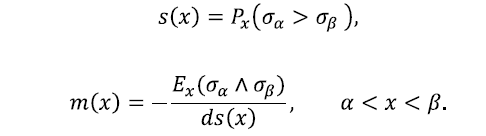
In the beginning, I wondered why he was repeating so simple computations
as exercises. However, in this way, he was bringing out intrinsic topological
invariants that do not depend on the differential structure. I understood that
the one dimensional diffusion is a topological concept but I was not as
thoroughgoing as Feller.
When Feller told me about this, he said he once listened to a lecture by Hilbert
who mentioned “Study a very simple case very profoundly, then you will truly
understand a general case.’’ I like to convey these words by Hilbert to you.”
Masatoshi Fukushima, Toyonaka Osaka
References
[D] J.L. Doob (1937), Stochastic processes depending on a continuous
parameter, Trans. Amer. Math. Soc. 42, pp. 107-140.
[I1] K. Itô (1942), On stochastic processes (infinitely divisible laws of
probability) (Ph.D. Thesis), Japan. Journ. Math. 18, pp. 261-301.
[I2] K. Itô (1942), Differential equations determining a Markoff process (in
Japanese), Journ. Pan-Japan Math. Coll. 1077 (English translation
in Kiyosi Itô Selected Papers, pp. 42-75, Springer, 1986)
[I3] K. Itô (1951), On stochastic differential equations, Mem. Amer. Math.
Soc. 4, pp. 1-51.
[K1] A. Kolmogorov (1933), Grundbegriffe der Wahrscheinlichkeitsrechnung,
Springer, Berlin.
[K2] A. Kolmogorov (1931), Über die analytischen Methoden in der
Wahrscheilichkeitsrechnung, Math. Ann. 104, pp. 415-458
[L] P. Lévy (1937), Théorie de l'Addition des Variables Aléatoires,
Gauthier-Villars, Paris.
Kiyosi Itô was born on September 7, 1915, in Hokuseicho, Mie prefecture,
Japan. He died last year on November 10, 2008, in Kyoto, at the age of 93.
Between these two dates lies an extremely successful career: in particular, the
creation of modern stochastic analysis with the central notion of the stochastic
integral in his paper from 1942, “On stochastic processes”, that provides a
probabilistic underpinning of Kolmogorov's analytical approach to diffusion
theory. Without these fundamental concepts, many areas of the theory of
stochastic processes that are the subject of this conference are unimaginable.
For his outstanding work, Itô received numerous prizes, and many honorary
doctorates. He was elected to the Academies of Sciences in Japan, the US and
France. Post-war Germany had no National Academy until recently. From our
perspective, Itô's work was honored by the Gauss prize
sponsored by IMU and DMV. And Itô received the renowned Israeli Wolf prize.
Only about half a year before Itô, on March 17, 1915, Wolfgang Döblin, second
son of the German-Jewish novelist Alfred Döblin, was born in Berlin. His family
emigrated to Paris in 1933 and Wolfgang became French. He studied mathematics at
the Sorbonne, did a doctorate with M. Fréchet in probability, was drafted for
the French army in 1938. When German troops were advancing in Eastern France in
summer 1940, his military unit in disarray, he took his life on June 21, 1940,
in a barn in Housseras, at the age of 25. In the last two of these 25 years,
during his military service, and in the period following the German attack on
Poland, known in France as la drôle de guerre, he had worked on a
manuscript which he decided to send as a sealed envelope (pli cacheté) to
the archive of the Académie des Sciences in Paris. He was never able to withdraw
the envelope himself, so his manuscript was shut away in the archive for 60
years, and made accessible only in 2000 after his brother Claude had given his
consent.
Though Itô and Döblin were born almost at the same time, it is hard to imagine
two more contrasting careers. If it comes to their mathematical goals, however,
surprising similarities appear. This is already indicated in the title of
Döblin's pli cacheté manuscript Sur l'équation de Kolmogoroff.
Roughly, as Bernard Bru and Marc Yor found out after it was opened in 2000 in
Paris, in the school pupils' exercise book in which Döblin had scribbled his
notes, were hidden elements of a weak form of Itô's stochastic approach to
Kolmogorov's parabolic PDE.
I cannot and do not want to be more specific on the relationship of the
mathematical work of Itô and Döblin at this point, and also not reveal more
about the tragic background story. To continue elaborating on this from the
mathematical perspective, I am glad and proud to present to you two outstanding
mathematicians, who have worked in the footsteps of both Itô and Döblin,
Masatoshi Fukushima from Osaka and Hans Föllmer from Berlin.
Masatoshi Fukushima received his Ph.D. with Kiyosi Itô as advisor. He is
globally known and renowned for his pioneering work at the interface of
stochastic processes and analysis, the mathematical field starting at
Kolmogorov's and Itô's approaches to the heat diffusion, with a modern focus on
Dirichlet forms. He will now talk about his impressions of the life and legacy
of his teacher Kiyosi Itô.
I am now very proud to announce my colleague Hans Föllmer. Hans is a globally
recognized pioneer in the area of stochastic analysis and finance. On the first
sight a different area, his work witnesses the striking efficiency of
mathematical concepts. Namely, Itô's and Döblin's work, starting in paradigms of
physics, can nowadays also be seen as fundamental for mathematical finance. Hans
will talk about Döblin's work and the link to Itô's.
We now return to the tragic background of Wolfgang Döblin's short career. I must
confess that during my years of study of Mathematics and Physics at the
University of Munich when I heard, in my first course on Markov processes, about
the famous Döblin coupling technique, I thought that the novel “Berlin
Alexanderplatz” had just been written by a multi-talent in literature and
mathematics. Only after 2000, French friends told me about the pli cacheté
and the tragic story of the writer Alfred's mathematician son Wolfgang. The
story left me dumbfounded when I first heard of it.
Probably the same happened to two journalists from Hamburg and Amsterdam, Agnes
Handwerk and Harrie Willems, who are both present in this room, and who got
seized by the extraordinary story. They first met with Bernard Bru, professor at
the university Paris 5. He reported about how in 1991 at the Acadèmie des
Sciences in Paris he came to know of the existence of a sealed envelope, while
preparing a meeting in the US in memory of Wolfgang Döblin, organized by Kai-Lai
Chung and Joe Doob. Bernard Bru encouraged the journalists to work on a
documentary about the story. They produced a radio presentation, followed by a
video film. It is this video film, also available as a DVD from Springer that we
will now present to you. Please enjoy it.
Peter Imkeller, Berlin
Further information about the conference event on Tuesday
featuring K. Itô and W. Döblin and the tragic story about the sealed envelope
can be found in
[1] M. Fukushima: On the works of Kiyosi Itô and stochastic analysis.
Japanese Journal of Mathematics 2 (2007), 45-53
[2] B. Bru, M. Yor: Comments on the life and mathematical legacy of Wolfgang
Doeblin, Finance and Stochastics 6 (2002), pp. 3-47.
[3] P. Imkeller, S. Roelly: Die Wiederentdeckung eines Mathematikers: Wolfgang
Döblin, Mitteilungen der Deutschen Mathematikervereinigung 15
(2007), pp. 154 - 159, ISSN 0947-4471.
[4] Rediscovered Proof: Wolfgang Döblin. IMS Bulletin 38 (3), pp.
8-9.
[5] Handwerk, H. Willems: Wolfgang Doeblin A Mathematician Rediscovered, DVD,
PAL, (English, French and German), Springer, Berlin 2007, ISBN
978-3-540-71959-5.